Area Of A 3d Object

In Geometry, a shape is divers as the figure closed past the boundary. The boundary is created by the combination of lines, points and curves. Basically, in that location are two unlike types of geometric shapes such as:

Two – Dimensional Shapes
3 – Dimensional Shapes

Each and every shape in the Geometry can exist measured using dissimilar measures such as area, volume, surface area, perimeter and and so on. In this article, permit united states discuss the area of shapes for 2D figures and 3D figures with formulas.

Table of Contents:

- Surface area Definition
- 2D Shapes
- Area of 2d shapes
- 3D shapes
- Area of 3D Shapes
- Examples

What is Area?

An surface area is a quantity that expresses the extent of a 2-dimensional figure or shape or planar lamina in the plane. Lamina shapes include 2d figures that tin be drawn on a plane, e.g., circle, square, triangle, rectangle, trapezium, rhomb and parallelogram. Area of shapes such equally circle, triangle, square, rectangle, parallelogram, etc. are the region occupied by them in space.

Polygon shape:A polygon is a ii-dimensional shape that is formed by direct lines. The examples of polygons are triangles, hexagons and pentagons. The names of shapes describe how many sides be in the shape. For case, a triangle consists of three sides and a rectangle has four sides. Hence, any shape that tin be formed using 3 straight lines is known as a triangle and any shape that tin can be drawn past linking 4 lines is known equally a quadrilateral. The area is the region inside the purlieus/perimeter of the shapes which is to be considered.

What are 2d shapes?

The 2-dimensional shapes (second shapes) are also known as apartment shapes, are the shapes having two dimensions merely. It has length and breadth. Information technology does not have thickness. The two different measures used for measuring the flat shapes are area and the perimeter. Two-dimensional shapes are the shapes that can be drawn on the piece of newspaper. Some of the examples of 2nd shapes are foursquare, rectangle, circle, triangle and so on.

Area of 2D Shapes Formula

In general, the surface area of shapes can be defined as the amount of paint required to cover the surface with a unmarried coat. Following are the means to summate area based on the number of sides that exist in the shape, as illustrated below in the fig.

Area Of Shapes

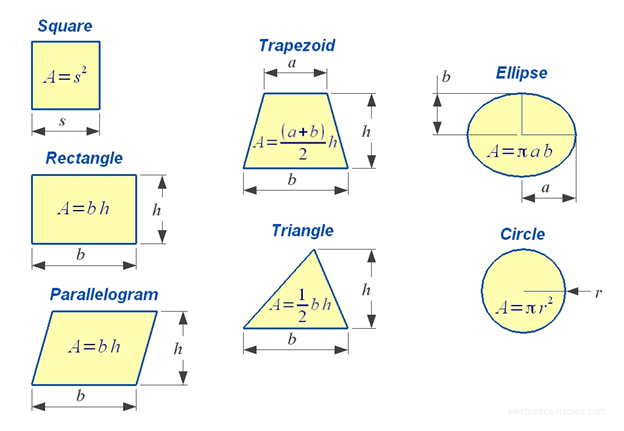
Let us write the formulas for all the unlike types of shapes in a tabular form.

Shape	Surface area	Terms
Circle	π × r ²	r = radius of the circle
Triangle	½ × b × h	b = base h = elevation
Square	a ²	a = length of side
Rectangle	l × w	50 = length w = width
Parallelogram	b × h	b=base of operations h=vertical height
Trapezium	½(a+b) × h	a and b are the length of parallel sides h = height
Ellipse	πab	a = ½ pocket-sized axis b = ½ major axis

Likewise, read:

Area And Perimeter
Area Of Rectangle
Areas Of Parallelograms And Triangles Grade 9
Areas Related To Circles For Form x

What are 3D shapes?

The three-dimensional shapes (3D shapes), known every bit solid shapes, are the shapes that accept three dimensions such as length, breadth and thickness. The two distinct measures used to define the 3-dimensional shapes are volume and surface surface area. Generally, the three-dimensional shapes are obtained from the rotation of 2-dimensional shapes. Thus, the surface surface area of any 2D shapes should be a 2D shape. If y'all want to calculate the surface area of solid shapes, we can easily calculate from the area of 2D shapes.

Area of 3D Shapes Formula

According to the International System of Units (SI), the standard unit of surface area is the square meter (written equally one thousand²) and is the area of a square whose sides are one meter long. For example, a particular shape with an area of three foursquare meters would take the same area every bit three such squares. The surface expanse of a solid object is a measure of the total area that the surface of the object occupies.

For 3D/ solid shapes like cube, cuboid, sphere, cylinder and cone, the area is updated to the concept of the surface area of the shapes. The formulas for three-dimension shapes are given in the table here:

Shape	Surface surface area	Terms
Cube	6a²	a = length of the edge
Rectangular prism	ii(wl+hl+hw)	l = length due west = width h = height
Cylinder	2πr(r + h)	r = radius of circular base of operations h = height of the cylinder
Cone	πr(r + l)	r = radius of circular base l = camber top
Sphere	4πr²	r = radius of sphere
Hemisphere	3πr²	r = radius of hemisphere

In addition to the surface area of the planar shapes, an additional variable i.eastward the superlative or the radius are taken into account for computing the surface area of the shapes.

Consider a circle of radius r and make endless concentric circles. Now from the centre to the boundary make a line segment equal to the radius and cut the figure forth with that segment. It'll be formed a triangle with base of operations equal to the circumference of the circumvolve and height is equal to the radius of the outer circle, i.eastward., r. The area can thus be calculated equally ½ * base * height i.e

½ * 2πr*r

Area of Shapes Examples

Example 1:

Discover the expanse of the round path whose radius is 7m.

Solution:

Given, radius of circular path, r = 7m

By the formula of area of circle, we know;

A =π r²

A = 22/7 x 7 ten 7

A = 154 sq.m.

Instance ii:

The side-length of a square plot is 5m. Observe the expanse of a square plot.

Solution:

Given, side length, a = 5m

By the formula of expanse of a square, we know;

Surface area = a ²

A = 5 x 5

A = 25 sq.m.

Example 3:

Discover the area of the cone, whose radius is 4cm and peak is 3cm.

Solution:

Given, radius of cone = 4cm

and top of cone = 3cm.

As per the formula of surface area of cone, we know;

Camber height =l = √(4^two + 3² ) = √25 = five cm

Area = πr(r + l)

= (22/seven) × iv(four + five)

=(22/7) 36

= 113. 14 cm^two

To learn more Maths-related articles, stay tuned with BYJU'S – The Learning App and download the app to acquire with ease past exploring more videos.